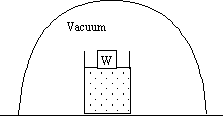
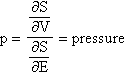James Hurley

I’m not quite sure what Keats had in mind in his Ode on a Grecian Urn when he wrote, “Beauty is truth, truth is beauty,—that is all ye know on earth…” While this is certainly not a universal truth, there came a time when I felt it had a certain application to my understanding of thermodynamics, the poor relations among the fundamental disciplines of physics.

In choosing to focus this issue on the teaching of thermodynamics, the Forum has made the perfect choice. There is no branch of physics more in need of rehabilitation than the teaching of thermodynamics.

As a student, many years ago, my initial impression of thermodynamics as a subject worthy of study was very low. I recall thermodynamics as that branch of physics in which one deliriously performed partial derivatives until the answer emerged as an apparition. It drove me adiabatic. It took a back seat to every other subject. But I was able to do the homework, solve the problems, and grunt my way through.

Alas, as I took up a career in teaching, I was faced with the tedious task of teaching the subject myself. It was a low point in my career. I confess that I taught the subject for many years before I developed any real understanding of it. I felt a need to reimburse those poor students who suffered under my tutelage.

So the energy was a state function, a function of a few fundamental physical parameters. So the entropy was a state function also. So what? There existed a whole menagerie of state functions: Energy, Entropy, Enthalpy, Gibbs and Helmholtz Free Energies, etc. Maybe, as in elementary particle theory, I could discover a new thermodynamic particle, a new state function, the Hurley I would name it; I would be famous. I was so naïve.

Needless to say, I felt badly about my ignorance. I had a nagging suspicion that I was missing the boat entirely. And then that day of enlightenment dawned when I came upon the work of J. Willard Gibbs. It was a revelation. Suddenly I understood, understood at a fundamental level, and began to appreciate that there is a beauty in thermodynamics, just as there is beauty in any synthesis, any reduction of diverse and divergent results to a single unifying principle. And in thermodynamics, that principle is intuitive! Glorious, astonishing, beautiful! Thermodynamics now stood apart from all other disciplines in physics as the only discipline in which we can understand the fundamental laws on an intuitive basis.

Why is there an Equilibrium State?

So how should thermodynamic law be introduced? No physical law should be divorced from the natural phenomena that it is meant to encompass. It is both a curse and a blessing that the phenomenon from which the postulates of statistical physics are best derived is so commonplace. Familiarity breeds oversights. The phenomenon of which I speak is that of the existence of the equilibrium state.

Observation: In the course of time, confined, isolated systems with large numbers of particles will reach an equilibrium state in which the macroscopic observables remain constant in time.

Understanding the physical basis for this phenomenon is the foundation of all statistical physics. The postulates of statistical physics grow out of the very existence of the phenomena to be studied, the existence of the equilibrium state. It must be recognized that this phenomenon—macroscopic variables of systems with large numbers of particles exhibiting an equilibrium state behavior—is something worthy of study and not a tautology.

So thermodynamic systems come to an equilibrium state. We therefore take for our first law (for a simple system): There exist equilibrium states of macroscopic systems that are completely characterized macroscopically by the internal energy, the volume, and the number of particles of the various constituents.

This seems like an unlikely physical law. First of all, there is no equation. Second, it is not obvious that it passes the basic test for a physical law: Can it make quantitative predictions on untried experiments? So what predictions can we make from the first law of thermodynamics without any equations?

Experiment: Take any macroscopic system. Heat it, compress it, cool it, expand it, but eventually bring it back to its original energy and volume and keep the particle numbers the same.

Prediction: All macroscopic observables will return to their original values, not just the energy, volume and particle numbers.

Another way to look at the first law is that it describes the dimension of the thermodynamic state space. By dimension I mean the number of independent variables.

The first law of thermodynamics establishes the playing field, but we need a second law to determine the rules of the game. To see what the game is and how this second law will help, imagine two blocks with given internal energies brought into thermal contact; how is the energy shared between the two blocks when the equilibrium state is reached?

Let us approach the distribution of energy problem from a statistical point of view. The first law tells us only the relevant variables—those variables that determine the macrostate. We need a law that predicts how these variables change after the two blocks are brought together and come to a new final state.

Here we make a conjecture as to the reason for the equilibrium state. The first law recognized the existence of the equilibrium state. The second law expresses a rationale.

Observation:
For most large systems there is one macrostate that is associated with a great many microstates, while other macrostates are associated with comparatively few microstates. As the system evolves in time from one microstate to another, it will more often than not be found in the macrostate with the most associated microstates. Since the system is most often found in the same macrostate, it will be in a steady state, or equilibrium state. The equilibrium state is the macrostate with the most associated microstates.

Can we postulate a second law of thermodynamics that will encompass this speculation? We can, and that law is the second law of thermodynamics: For all macroscopic systems there exists a function (called the entropy and denoted symbolically by S) that is defined for all equilibrium states, i.e., all possible values of the energy, volume, and particle numbers. The entropy of a composite system is the sum of the entropies of the components. In the absence of an internal constraint, the values assumed by the energies, volumes, and particle numbers of the components in a closed system are those that maximize the total entropy.

Or, the short form: The entropy of the system in the equilibrium state will be as large as the constraints allow.

The reason an equilibrium state is reached is that there is one macrostate with a very large number of associated microstates. All we have really done is substitute the word entropy for the phrase number of associated microstates and assumed that the measure of the number of microstates is a function of the variables that determine the macrostate and that the measure can be made additive.

In general we stand in awe of the laws of nature. Although we may be able to articulate these laws, we have no fundamental understanding of their origin. We know not why light resolutely, indeed jealously, travels with a fixed speed, which no other may exceed and that this speed appears to be the same for all observers regardless of their relative motion. It is a wonder to behold but not as yet understood. We know not why matter is quantized and is willing to subject itself to something so bizarre as a wave equation. And why gravity? Why do bodies exhibit gravitational attraction proportional to their inertial properties? And what is energy? Feynman said, “It is important to realize that in physics today, we have no knowledge of what energy is.” We stand in awe of such wonders, but we do not yet understand them at a fundamental level.

But the second law is different. It is every man’s law. Every poker player, every housekeeper has a feeling for it. It follows from the laws of probability. The only mathematics required to understand this law is the ability to count. Frequency of occurrence is proportional to the probability. Throw a hundred coins in the air and every person can predict the likely outcome: about the same number of heads and tails without knowing anything about gravity or the laws of motion governing tumbling coins. There are a lot more ways of achieving half heads and half tails than any other ratio. The second law of thermodynamics is all about counting. It is the only law of nature for which we have this level of intuition.

I have said nothing about energy conservation as thermodynamic law. Thermodynamics deals only with statistical law. There is nothing statistical about energy conservation, just as there is nothing statistical about the conservation of mass, momentum, or electrical charge.

How is Entropy Measured?

We have said that the entropy in the equilibrium state is as large as the constraints allow. We know how to use this law to predict the results of experiment. For example, when we put two bodies at different temperatures together and allow them to exchange heat, we can predict that they will eventually come to the same final temperature and we can determine what that temperature will be by maximizing the entropy functions—provided of course that we know the entropy functions of the two bodies. But there’s the rub. There is nothing in our statement of the second law that appears to define the entropy—all we know is that the entropy of any system in equilibrium is as large as the constraints allow. (It’s something like Newton’s laws of motion. There is no definition of force except F = ma. So where is the law? It should be that the observable, so defined, is a state function, a function of the kinematic state of the system. But I digress.)

We need to show that that is enough. We need to devise an operational procedure by which we might measure the entropy of any system for any values of its thermodynamic variables. Knowing this entropy function, we may use it to determine how this system will interact with any other known system.

I shall make this very brief, first proving that dS = dQ/T for a simple system and then showing how this equation may be used to determine the entropy. We will use only the fact that the entropy is a maximum in the equilibrium state..

Consider a substance, a gas for convenience, confined to a cylinder with a weight W on the lid. See figure below. When the equilibrium state is reached the entropy will be a maximum, i.e. dS = 0 for any displacement compatible with the constraints, perhaps a slight elevation in the lid.

Since the entropy depends only on the energy and volume—a consequence of the first law—we know that the resulting change in entropy due to a change in energy and volume is given by:

We define T by the equation

and p by the equation:

For the moment these are only definitions.

(It is a simple matter to show that the entropy will be a maximum for two systems that can exchange energy when the value of T is the same for both systems. Likewise we can show that the values of p will be the same for two systems that can exchange volume. Therefore T and p are not unreasonable candidates for temperature and pressure.)

With these definitions we may write:

Now when the piston is in the equilibrium state, the entropy is a maximum and so dS = 0 or

Since energy is conserved:

where z is the height of the weight W above the chosen ground level. For an infinitesimal change in the height of the piston,

dE + W dz = 0

We also know from the second law that

dE + p dV = 0.

Since dV = A dz where A is the cross sectional area of the piston, it follows that

But, by definition, the pressure within the cylinder is just the force per unit area on the piston so that we have finally

p = pressure

and we have a most important identification. We now know that

and so the ratio of these partial derivatives is a measurable quantity.

We have come part way in our quest for measurable entropy. We have

for arbitrary changes in internal energy and volume. But now dE, p, and dV are measurable. We don’t yet know how to measure T.

It is customary to separate the change in energy of a thermodynamic substance into two parts: one due to heat energy (dQ) added to the substance, and one due to mechanical work, in this case -p dV done on the substance. We may write

dE = dQ - p dV

This equation should properly be regarded as a definition of dQ. (If there are variations in molar numbers, we must include the sum of mi dNi.) The entropy change can then be written:

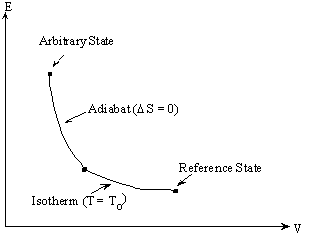
perhaps the most familiar relation in the mathematical expressions of the second law of thermodynamics. In this equation we can measure dQ but not T—yet. But this is quite straightforward. Choose any reference state and define its temperature to be To. Since dQ is measurable, one can determine the entropy along the isotherm through the reference state—see the figure. The entropy of any arbitrary state along the adiabat will be equal to the entropy at the point of intersection with the isotherm through the reference state.

Having determined the entropy everywhere we can evaluate the temperature anywhere by calculating the partial derivative of the entropy with respect to the energy. We have therefore succeeded in our task: We have shown that dS = dQ/T where dQ and T are measurable. We have used only the defining property of the entropy: It is that function of the energy E and the volume V that is a maximum in the equilibrium state.

I have taught thermodynamics from this point of view at the introductory level (see Principles of Physics by James Hurley and Claude Garrod (1978), the upper division level (course notes: Statistical Physics 1987) and finally in a possibly futile attempt at the level of the interested, perhaps obsessive, layman in A Paradox in Time by James Hurley (2004). This last book, however, focuses on a resolution of the time-asymmetry paradox.)

James Hurley is Professor Emeritus at the University of California, Davis He can be reached at jhurley@infs.net. A Paradox in Time is available at Amazon.com.